This section introduces foundational concepts of calculus and vectors, essential for STEM fields. It explores limits, derivatives, integration, and vector operations, providing a comprehensive overview for students beginning their study.
1.1 Overview of the Nelson Calculus and Vectors 12 Textbook
The Nelson Calculus and Vectors 12 textbook is a comprehensive resource designed for Grade 12 students pursuing STEM fields. It integrates calculus and vector concepts, starting with foundational topics like limits, derivatives, and vector operations. The textbook is structured into 12 chapters, covering essential skills such as simplifying expressions, solving equations, and advanced calculus topics like integration and parametric functions. Vectors are introduced early, emphasizing their applications in physics and engineering. The textbook aligns with the Ontario curriculum, making it ideal for students preparing for post-secondary studies. Accompanying the textbook is a detailed solutions manual, providing step-by-step answers to exercises and review questions. This resource helps students master complex concepts and builds confidence in problem-solving. The textbook also includes practical applications and real-world examples, reinforcing the relevance of calculus and vectors in modern science and technology.
1;2 Importance of Calculus and Vectors in STEM Fields
Calculus and vectors are cornerstone disciplines in STEM fields, providing essential tools for analyzing and solving real-world problems. Calculus enables the study of rates of change, optimization, and accumulation, crucial in engineering, physics, and computer science. Vectors extend these concepts into multiple dimensions, facilitating applications in fields like robotics, aerospace, and data science. Together, they form the mathematical foundation for modeling complex systems, from population dynamics to fluid mechanics. Proficiency in these areas is vital for innovation and advancement in technology, medicine, and scientific research. The Nelson Calculus and Vectors 12 textbook prepares students for these challenges, ensuring they are well-equipped to pursue careers in STEM disciplines. By mastering these subjects, students gain the ability to approach problems analytically and develop innovative solutions, making calculus and vectors indispensable in their academic and professional journeys.

1.3 Structure of the Textbook and Solutions Manual
The Nelson Calculus and Vectors 12 textbook is structured to align with the curriculum, offering a logical progression from foundational concepts to advanced topics. The textbook is divided into 12 chapters, each focusing on specific areas such as limits, derivatives, integration, and vector operations. The accompanying solutions manual provides detailed, step-by-step explanations for exercises in each chapter, ensuring students can review and understand complex problems. Additional resources include practice exams, video explanations, and interactive tools, all designed to enhance learning. The textbook’s clear organization and comprehensive coverage make it an invaluable resource for students aiming to master calculus and vectors. By following this structured approach, learners can build a strong foundation and confidently tackle challenges in STEM fields.

Key Chapters in the Textbook
The textbook features chapters on limits, derivatives, integration, and vector operations, providing a structured approach to mastering calculus and vectors for STEM applications.
Chapter 1 provides a foundational overview of calculus, introducing key concepts such as limits, derivatives, and the difference between differential and integral calculus. It explores the historical development of calculus and its significance in STEM fields. The chapter also reviews prerequisite skills, including functions, graphs, and trigonometric relationships, ensuring students are prepared for advanced topics. Practice problems and solutions are included to reinforce understanding of basic principles. This chapter sets the stage for more complex concepts in subsequent chapters, such as rates of change and vector operations. The solutions manual offers detailed explanations for each exercise, helping students grasp fundamental ideas. By mastering this chapter, learners build a solid foundation for their calculus and vectors journey.
2.2 Chapter 3: Derivatives and Their Applications

Chapter 3 delves into the core concept of derivatives, explaining their definition, rules, and practical applications. It covers essential topics like power, product, quotient, and chain rules, enabling students to compute derivatives of various functions. The chapter also explores real-world applications, such as optimization, related rates, and motion along a line. Step-by-step solutions in the manual guide learners through complex problems, ensuring clarity and understanding. This chapter is crucial for developing problem-solving skills in calculus, preparing students for advanced applications in STEM fields. The detailed explanations and practice exercises make it an indispensable resource for mastering derivatives and their applications.
2.3 Chapter 5: Derivatives of Exponential and Trigonometric Functions
Chapter 5 focuses on the derivatives of exponential and trigonometric functions, crucial for advanced calculus topics. It introduces the derivatives of e^x, ln(x), sine, cosine, and tangent functions, along with their inverse counterparts. The chapter emphasizes the importance of these functions in modeling real-world phenomena, such as population growth and wave patterns. Step-by-step solutions in the manual provide clear guidance on differentiating these functions and applying them to various problems. Practice exercises and examples help reinforce understanding, making this chapter a vital component of the curriculum. The content is supported by detailed explanations and resources, ensuring students grasp these fundamental concepts necessary for further studies in calculus and related fields.
Chapter 6 provides a foundational understanding of vectors, their properties, and operations. It introduces students to vector notation, types of vectors, and essential concepts like magnitude and direction. The chapter explains vector addition, scalar multiplication, and the dot product, with practical examples to illustrate their applications. Geometric interpretations are emphasized to help visualize vector relationships. The solutions manual offers detailed explanations for exercises, ensuring students master these foundational skills. This chapter is critical for understanding more complex topics in subsequent chapters, such as equations of lines and planes. By focusing on both theoretical and practical aspects, Chapter 6 establishes a strong basis for advanced vector analysis in STEM fields.
2.5 Chapter 8: Equations of Lines and Planes
Chapter 8 focuses on the equations of lines and planes, a fundamental topic in vector calculus. It explores how to define and represent lines and planes in three-dimensional space using parametric equations and Cartesian forms. Students learn to determine the equation of a line given two points or a point and a direction vector, as well as the equation of a plane using three points or a normal vector. The chapter also covers finding the distance from a point to a line or plane, which is crucial for solving real-world problems in geometry, engineering, and physics. Practical applications and detailed solutions in the manual help reinforce these concepts, ensuring a solid understanding of spatial relationships and their mathematical representations. This chapter builds on earlier vector concepts, preparing students for advanced topics in multivariable calculus.
2.6 Chapter 9: Relationships Between Points, Lines, and Planes
Chapter 9 delves into the intricate relationships between points, lines, and planes, a cornerstone of spatial understanding in vector calculus. It examines how lines can be parallel, intersect, or skew relative to planes, and vice versa. Students learn to determine if a line lies on a plane or is parallel to it, as well as how to find the intersection point of a line and a plane. The chapter also explores the concept of orthogonality and how vectors can describe these spatial relationships. Practical problems, such as finding the distance from a point to a plane, are solved using vector methods. Detailed solutions in the manual guide students through these geometric analyses, reinforcing their ability to visualize and compute in three-dimensional space. This chapter is vital for understanding advanced topics like projections and orthogonality in multivariable calculus.

Detailed Solutions Manual
The solutions manual provides detailed explanations and step-by-step answers for all chapters, ensuring clarity and understanding of complex calculus and vector concepts. It aligns with the textbook, covering Chapters 1-12.
3.1 Chapter 1 Solutions: Review of Prerequisite Skills
Chapter 1 focuses on reviewing essential math skills necessary for success in calculus and vectors. The solutions manual provides detailed explanations for simplifying expressions, solving equations, and understanding functions. It covers key topics like algebraic manipulation, graphing, and analyzing polynomial and rational functions. Step-by-step solutions are included for problems involving inequalities, systems of equations, and trigonometric identities. The manual also addresses logarithmic and exponential functions, ensuring students grasp these foundational concepts. Additional resources, such as practice exams and online solutions, are available to reinforce learning. The clear, structured approach helps students build confidence and prepare for more advanced topics in calculus and vectors. The solutions are aligned with the textbook, making it easier for students to follow and understand the material.
3.2 Chapter 6 Solutions: Vectors Review
Chapter 6 delves into the fundamentals of vectors, a critical component of calculus. The solutions manual offers comprehensive explanations for vector operations, including addition, subtraction, and scalar multiplication. It also covers the dot product, cross product, and vector applications in geometry and physics. Detailed solutions are provided for problems involving vector magnitudes, directions, and resolutions. The manual emphasizes the importance of understanding vector representations and their graphical interpretations. Practice exercises and online resources are available to reinforce vector concepts, ensuring students can apply them confidently in subsequent chapters. The structured approach in the solutions manual aligns with the textbook, making it an invaluable resource for mastering vectors. Additionally, corrections and updates are included to address any textbook errors, ensuring accuracy and clarity in learning vector concepts. This review equips students with the skills needed for advanced vector applications in STEM fields.

3.3 Calculus Review Solutions
The Calculus Review Solutions provide a thorough recap of essential concepts, ensuring a strong foundation for advanced topics. It covers limits, continuity, and the fundamental theorem of calculus. Detailed explanations for derivatives and their applications, such as optimization and related rates, are included. The section also addresses integration techniques, including substitution and integration by parts. Key applications like area under curves and volumes of solids are explored. Practice problems and step-by-step solutions help students master these concepts. Additionally, corrections and updates to the textbook are provided to ensure accuracy. Online resources, such as video explanations, offer further support for complex topics. This review is designed to prepare students for the challenges of calculus, reinforcing their understanding and problem-solving skills.
3.4 Step-by-Step Solutions for Derivatives and Applications
This section offers comprehensive, step-by-step solutions for derivatives and their practical applications. It begins with the basics of differentiation, covering rules such as the power rule, product rule, and quotient rule. Detailed explanations are provided for implicit differentiation and logarithmic differentiation, ensuring clarity. Real-world applications like motion along a line, related rates, and optimization problems are thoroughly addressed. Each solution is broken down into manageable parts, making complex concepts accessible. Online resources, including video tutorials, supplement the textbook, offering alternative learning pathways. This section is designed to build confidence in applying derivative concepts to various scenarios, preparing students for advanced calculus topics and STEM applications. The structured approach ensures that students grasp both the theory and practical implementation of derivatives.

Additional Resources and Tools
Supplement your learning with online solutions manuals, video explanations, and practice exams; Interactive tools and expert resources provide comprehensive support for mastering calculus and vectors concepts effectively.
4.1 Online Solutions Manuals and PDF Downloads
, Chapter 6: Vectors Review, and advanced topics like derivatives and integration. Platforms like Quizlet and JholaBharke offer free and paid resources, ensuring students can review and practice effortlessly. Additionally, websites such as Z-lib.org provide downloadable PDF versions of the solutions manual, allowing offline access. These tools are invaluable for self-study, homework help, and exam preparation, covering everything from logarithmic differentiation to Gauss-Jordan elimination. By leveraging these resources, students can deepen their understanding and improve their problem-solving skills in calculus and vectors.
4.2 Video Explanations and Expert Educator Resources
. These videos provide clear, concise explanations of complex concepts, making them ideal for visual learners. Additionally, expert educators share tips and strategies for mastering calculus and vectors, ensuring a deeper understanding of the material. Many resources are available online, allowing students to access them anytime. These video explanations are particularly helpful for topics like logarithmic differentiation and Gauss-Jordan elimination, offering a dynamic approach to learning. By leveraging these tools, students can supplement their textbook studies and achieve academic success.
4.3 Practice Exam Questions and Answers
and Chapter 6: Vectors Review. By practicing with these materials, students can build confidence and mastery of key concepts before taking their final exams.
4.4 Interactive Tools for Calculus and Vectors
Enhance your learning experience with interactive tools designed for calculus and vectors. Platforms like GeoGebra and Desmos offer dynamic graphs and simulations, allowing you to visualize concepts such as derivatives, integrals, and vector operations. These tools enable you to experiment with equations, observe changes in real-time, and explore geometric relationships. Additionally, some resources provide step-by-step solvers that guide you through complex problems, breaking them down into manageable parts. Interactive quizzes and games are also available to make studying engaging. These tools are particularly useful for understanding topics like equations of lines and planes and relationships between points, lines, and planes. By leveraging these interactive resources, you can deepen your understanding and develop problem-solving skills in a hands-on environment.

Appendices and Supplementary Material
The appendices provide additional resources, including Logarithmic Differentiation and Gauss-Jordan Elimination guides. Supplementary materials also include corrections and updates to the textbook for accuracy and clarity.
5.1 Calculus Appendix: Logarithmic Differentiation
The Calculus Appendix in the Nelson textbook provides a detailed explanation of logarithmic differentiation, a powerful technique for differentiating complex functions. This method is especially useful for functions that involve products, quotients, or compositions of exponentials and logarithms. The appendix includes step-by-step examples and exercises to help students master this advanced differentiation skill. Key concepts such as simplifying expressions using logarithmic properties and applying the chain rule are emphasized; The appendix also addresses common challenges students face when dealing with logarithmic differentiation, offering practical tips and solutions. By working through the provided problems, students can gain confidence in their ability to tackle even the most intricate calculus problems involving logarithmic differentiation.
5.2 Vector Appendix: Gauss-Jordan Elimination
The Vector Appendix in the Nelson textbook includes a detailed section on Gauss-Jordan Elimination, a fundamental method in linear algebra for solving systems of linear equations. This technique is particularly useful for simplifying augmented matrices and finding solutions to vector-related problems. The appendix provides step-by-step instructions and examples to help students master this process. It emphasizes the importance of matrix operations and row reduction, which are critical skills for advanced vector applications. Practical problems are included to reinforce understanding, allowing students to apply Gauss-Jordan Elimination in various contexts. This section is essential for students aiming to solve complex systems of equations and prepares them for more advanced topics in vectors and linear algebra.
5.3 Corrections and Updates to the Textbook

The Nelson Calculus and Vectors 12 textbook includes a section dedicated to corrections and updates, ensuring accuracy and clarity for students. This appendix provides a detailed erratum listing any typographical errors, misprints, or content revisions made in the textbook. It also includes updates to problems, examples, and theoretical explanations to reflect the most current teaching methods and standards. Students can access these corrections through the official publisher’s website or via the accompanying digital resources. The updates are designed to enhance understanding and ensure that the material aligns with modern STEM education requirements. Regularly checking these corrections is highly recommended for students to maintain accuracy in their studies and solutions.
The Nelson Calculus and Vectors 12 textbook and solutions manual provide a comprehensive foundation for mastering STEM-related math concepts. With detailed explanations and resources, students can confidently progress in their studies.
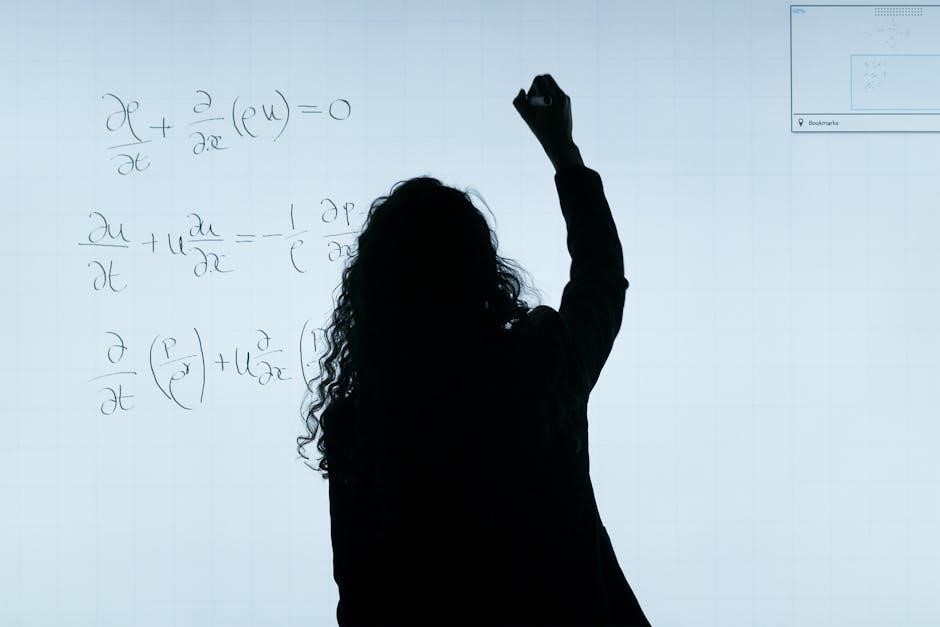
6.1 Summary of Key Concepts and Resources
This section summarizes the essential concepts covered in the Nelson Calculus and Vectors 12 textbook, including limits, derivatives, integration, and vector operations. It highlights the importance of these topics in STEM fields and provides an overview of the resources available, such as the solutions manual, which offers detailed step-by-step explanations for each chapter. Additional resources like online PDFs, video explanations, and practice exam questions are also noted as valuable tools for mastering the material. The textbook’s structure, along with its supplementary appendices, ensures a comprehensive understanding of both calculus and vectors. These resources collectively support students in achieving proficiency in advanced mathematical concepts.
6.2 Final Tips for Mastering Calculus and Vectors
To excel in calculus and vectors, consistent practice and a deep understanding of foundational concepts are crucial. Start by mastering limits, derivatives, and integration, as these form the backbone of calculus. For vectors, focus on vector operations and their geometric interpretations. Regularly review problem-solving strategies and seek guidance from resources like the Nelson Calculus and Vectors 12 solutions manual and online video explanations. Break complex problems into simpler steps and use graphical tools to visualize concepts. Additionally, practice with past exam questions to build exam readiness. Stay organized, track your progress, and don’t hesitate to consult with educators or peers for clarification. With dedication and the right resources, you can confidently master both calculus and vectors.